

Parabolic mirror surfaces are found wherever energy needs to be focused efficiently and accurately. You find them built into car headlights, spotlights as well as astronomical telescopes. Here we explore the parabola to design solar heaters.


The Parabola
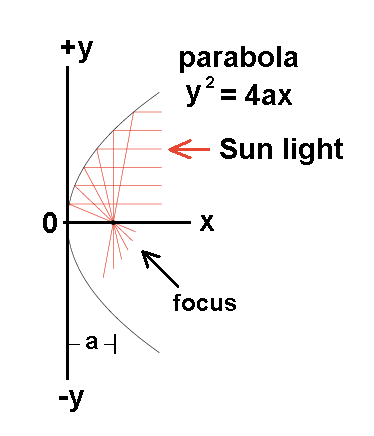
When Sun light (parallel rays) falls onto a correctly aligned parabolic mirror it will be reflected back towards a single point known as the focus. The parabolic mirror therefore directs the energy arriving over its surface to a 'hot spot' at the focus. You can use this energy to heat something.
The basic shape of a parabola is derived from the equation:
y² = 4ax [1]
Where y represents the distance away from the mirror centre and x represents the 'height above' the centre, see figure 1 and 2. The constant a is known as the focal length - the distance from the origin to the focus point.
If we want to make a parabolic reflector to our own particular specification i.e. in terms of its size D (i.e. having maximum y = D/2), height h and focal length a, then equation 1 becomes:
a = D²/16h [2]
A simple curved plane (rather than dish shape) solar heater is shown in photo 1 and we shall use this as an example, of course what follows can also be used for a full 'dish shaped' parabola and for much larger designs.
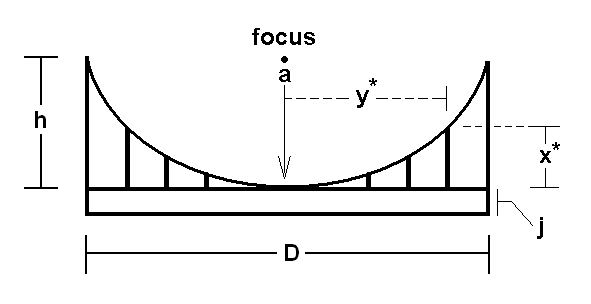
To make it easy to locate the focal point when we are using it, I chose to design the mirror surface height (h) to be the same value as a - the focus distance above the canter of the mirror (so a = h in this example 11 cm). In this case finding the focus is simple - imagine a line going across the top of the device, the centre of this line is where the focus is.
Rearranging equation 2 we get the diameter / length of the solar heater D to be:
D² = 16ah, so using h = a = 11 cm we get:
D = √(16x11x11) = √(1936) = 44 cm
We have y² = 4ax and a = 11 cm
For the solar heater shown in photo 1 we get x = y²/44
[3]
(all dimensions in cm)
Now that we have chosen the basic quantities for the parabola we can compute the x and y coordinates from equation 1 and 3. Some of these are tabulated in table 1. To re-cap, the y axis represents the distance away from the mirrors centre while x represents the 'height' above the base, the lowest point of the mirror (its centre).
You can also make a parabola support by cutting two side (parabola shaped) templates, see photo 1. In this case when marking up simply add a few cm (j in figure 2) to all the x values otherwise the template will diminish to zero thickness at the centre and it will all fall apart!
| ±y (cm) | y² | y²/44 | x (cm) |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1/44 | 0 |
| 2 | 4 | 4/44 | 0.1 |
| 3 | 9 | 9/44 | 0.2 |
| 4 | 16 | 16/44 | 0.3 |
| 5 | 25 | 25/44 | 0.6 |
| 6 | 36 | 36/44 | 0.8 |
| 7 | 42 | 42/44 | 0.9 |
| 8 | 64 | 64/44 | 1.5 |
| ... | ... | ... | ... |
| 20 | 400 | 400/44 | 9.1 |


Rough Science solar heater
In the second BBC TV Rough Science series Ellen McCallie and I made a large solar heater. A piece of straight wooden plank was cut for the base (D=2m). The central half way point was marked. At ±y cm distances every 15 cm or so, from the centre, vertical battens were attached having heights of x cm. When these were all in place a thin piece of plywood was put over the top to complete the parabolic surface. Our mirror had a surface area of about 1m2.
Mirrors
Various mirror surfaces can be used to cover the parabola surface. The Rough Science device used fragments of broken mirror cemented to the parabolic surface (see Note 1 below). I have also used small 3 cm mirror squares from an arts supplier as well as aluminium kitchen foil (see note 4). Flexible mirrored plastic sheet is also available which has excellent properties, it can also be cut with scissors and is very safe, easy to manipulate and change.
Locating the Sun and setting up the device
Obviously there needs to be direct sunlight to get any decent heating from the reflector but it is also important that the device is correctly aligned to the Sun. If the base can be extended a little and a bolt fixed through so that it points out at right angles then the bolts shadow should disappear when the device is pointing directly at the Sun. Obviously you can also adjust the hot spot for maximum brightness by trial and error.
What to heat?
At the equator there is about 1kW of solar power for every square meter of collecting surface. The small heater shown in photo 1 only has an area of about 1/20th m² but it still makes a good demonstration. Larger parabolic system having say 1-2 m² surface area should have enough energy to boil water in a small kettle for a cup of tea! The amount of heating obviously depends on the time of year / day, the weather and 'strength' of the sun (your latitude). Painting the kettle mat black with fire proof paint helps. Putting a large transparent plastic bag around the kettle also helps reduce heat loss (it acts like a mini green house). It would be fun to try cooking an egg on a flat plate arranged at the focus.
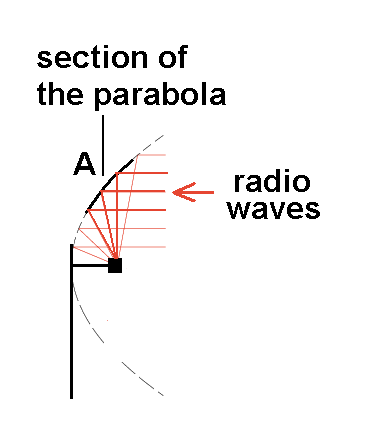
The satellite dish
Energy falling on to a correctly aligned parabolic mirror (of collecting surface area A) will be reflected to the focal point. However if you heat something large at this focus it will block the light getting to the mirror, effectively reducing A. There is a way of getting around this problem however.
Imagine a giant parabolic dish most of which we cut away to leave behind just a parabolic section of area A, near to the circumference. This remaining section will collect the same amount of energy as an ideal (full) parabola of the same area. Any energy falling on to this section would still be reflected to the focus point although now this point seems rather off-set from the dish. This is a useful modification as equipment put at the focal point will now not block the arriving energy. This technique is often used in satellite TV receiving dishes where the TV receiver head (a small electronic device) is placed at the focus (which now seems off-set) so the equipment does not block the path of the weak TV signals coming in from the space satellites (see above).
References
VHF / UHF manual, 4th Edition, G. R. Jessop, RSGB. ISBN 0 900612 63 0
The Rough Science solar heater - link to YouTube video
Notes
1. In the second of the BBC/OU Rough Science TV series, Ellen McCallie and I made a large parabolic water heater out of broken mirror fragment cemented onto a parabolic shaped wooden base. We used a blacked kettle at the focus and it was easy to align the contraption to boil water in 10 minuets or so.
2. Ellen and I tried very hard to get the maths of the parabolas into the Rough Science TV series. We even went away and practised till we got a description down to a nippy 20-30 seconds but all our efforts hit the 'cutting room floor'. It seems to be very difficult to get maths on TV, even when it has a direct and relevant application.
3. For a full shaped parabolic dish aligned correctly a line drawn from the mirror centre out through the focus point will point directly to the Sun. In the case of a satellite dish, which is not a whole round parabola, you can't locate the satellite in the same way. In this case in the UK the Satellite is far higher in the sky and you have to imagine the radio waves coming down, hitting the parabolic section and then being reflected downward again to the receiver.
4. You can use old discarded satellite dishes to make solar heaters. Cover the dish in kitchen foil (note foil usually has one side more shinny than the other) and place a kettle (or other object to be heater) where the receiver head used to be. Then move the dish till the brightest spot gets reflected onto the kettle. On a summers day in the UK the dish will obviously have to be aligned at the Sun but it will also probably be at a similar angle to that used for satellites (look around you to see the angle of neighbours dishes).
5. How accurate does the parabola template need to be? If you want to make a telescope then the answer is very accurate, perhaps to better than 1/100 mm. Our wooden supported mirrors will not be so accurate and so will tend to give a larger spot of light at the focus than the ideal. The Rough Science heater, for example, not being a true dish but a curved plane, gave a 'line' rather than 'spot' of light. This might give a more uniform heating effect though than a very tiny intense spot. In the Death Valley series of Rough Science TV Kathy Sykes made a solar heater by rolling up a polished metal sheet (or foil) into a large cone shape and using this approximate parabola to great effect.
THE CREATIVE SCIENCE CENTRE
home | diary | whats on | CSC summary | latest news