Newtons Experiments - Three circles

Three uniform circles about 20 cm in diameter and 10mm thick have been made out of wood and varnished. The circles have holes drilled through them so that they can be fitted into the calipers. The calipers have two adjustable screws that can be aligned and fixed into position over the holes so that the discs can be held and also rotated.

If a hole is drilled in the center of a body and it is allowed to rotate around this axis we call this the center of motion. If the body is a perfect circle and made of uniform material then this center of motion will also be the center of mass - more commonly called the center of gravity.

Experiment 1
The first circle (shown in the middle on the photo) has a hole drilled exactly in the middle. When fitted into the calipers the disc freely spins around the axis hole. If the disc is stopped at any position the disc remains where its is stopped, it does not rotate back or forth. As the center hole is also the center of the mass of the wooden circle we find in this first simple case that the center of motion is also the center of gravity of the disc. The disc is in equilibrium whereever it happens to be; still or spinning.

Experiment 2
The second disc (left hand side of photo) is identical to the first disc but also includes another hole off set from the center. With the callipers set on the first hole we have exactly the same situation as in experiment 1. With the callipers set on the second (off-set from the center) hole we find that when the disc is spun it wobbles around its new center of motion. As this is now no longer the true center of mass the disc is unbalanced. If we stop the spinning disc at random it is likely to rotate a little further until it reaches equilibrium. We find that there are two equilibrium points where the disc can be stopped and where it does not try and rotate.

If we hold a plum line over the disc, aligned so that the string passes through the point of support by the calippers, the two equilibrium points are above and below the support points intersected by the plumb line on the disc. At these two points the disc will stay put and not rotate.

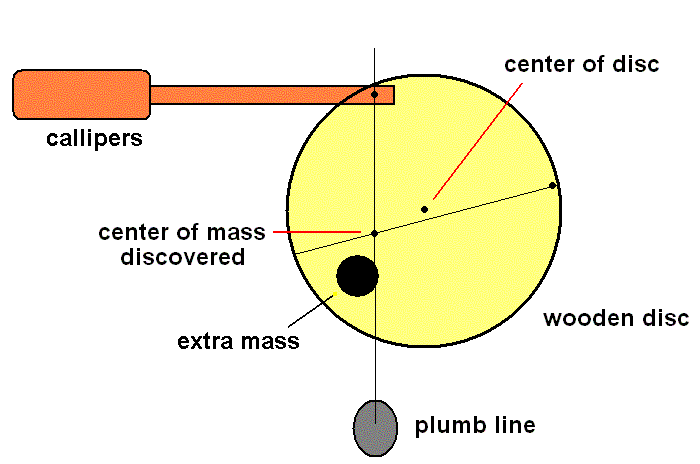
Experiment 3
The final disc (right hand side of photo) has a hole drilled in the exact center but it also has an extra weight imbeded at some point within the disc (not at the center). There are also two holes drilled in random positions near to the circumference and one drilled off set from the center (see below).

Even though the hole is at the center of motion it is not at the center of mass anymore because of the extra mass. Consiquently it rotates when fitted into the calippers just as the offset hole did in Experiment 2. In order to balance this disc (wheel) we need to find the new center of mass. We do this in a very simple manner. Remove the disc from the calipers and fit it into one of the random holes near to the circumference. Allow the disc to fall / rotate till it stops, i.e. the second equilibrium point, as it did in experiment 2 for the offset disc. Using the plum line whose string goes through this point of support on the callipers, draw a line across the disc downward. The new center of mass must lie somewhere along this line.

Re-fit the disc into the callipers at the other random piont and do the same thing with the plumb line, drawing a line across the disc. The new center of mass must also lie somewhere along this line too. The only place where the center of mass lies on both these lines must be where the two lines intersect. At this point you will notice I have drilled a final hole. This is the center of mass for this particular modified disc. When its is hung from this point (instead of the exact center) we find it is balanced and in equilibrium.

If it is set up in the callipers we see that even though the disc wobbles when it is rotated it moves very smothly and wherever it happens to stop it is in equilibrium and does not rotate any further one way or the other. This method of finding the center of mass can be used on any shape. Note however that if the disc is not uniform across the width of the disc the center of mass might be offset on the axis of rotation.