
Summary
In this article we explore the shape, symmetry and surface structure
of a football to see how this understanding can help us draw these sort of complex shapes.


Drawing
We all know that drawing is not always as easy at it looks. Sometimes, however a few tricks can really help us draw more effectively. For example, knowing that the eyes are roughly halfway down the head can really help drawing a realistic face. Rules like these can transform our ability to draw. What follows is an exploration of the structure (the detailed shape) of the 'common or garden' football. We do this so that we can find simple rules that will enable us to draw this familiar object more realistically. What we learn could be applied to drawing all sorts of other symmetrical objects and shapes.
We think we know a football
We have all seen footballs 100's of times - they should be easy to draw. But when we try we tend to get into trouble. We vaguely know that there are patches of different shapes and colours on the round ball. But then when we come to draw it we realise that we don't actually know the structure very well at all. Just like the various rules artists use for drawing we can uncover the structure behind the football and so help us draw it more accurately.
Seeing things clearly - Observation
To accurately observe what is in front of us is surprisingly difficult. We are so used to seeing things that we often get lazy and rather than 'looking and seeing' we tend to anticipate (from past experience) what we think is really there.
Both the scientist and the artist need to clearly observe in order to progress - in that sense they have a lot in common. This process can be seen so well in the work of Leonardo da Vinci.
In Michael White's wonderful book "Leonardo the first Scientist" he quotes Leonardo's observations of how waves are set up in water when a pebble is thrown in. What is remarkable about the writing is the clarity of da Vinci's observation:
"If you throw two small stones at the same time on a sheet of motionless water at some distance from each other, you will observe that around the two percussions numerous separate circles are formed; these will meet as they increase in size and then penetrate and intersect one another, all the while maintaining as their respective centres the spot struck by the stones. And the reason for this is that the water, although apparently moving, does not leave its original position, because the opening made by the stones closes again immediately. Therefore the motion produced by the quick opening and closing of the water has caused only a shock which may be described as a tremor rather than movement. In order to understand better what I mean, watch the blades of grass that because of their lightness float on the water, and observe how they do not depart from their original positions in spite of the waves underneath them caused by the occurrence of the circles. The reaction of the water being in nature of tremor rather than movement, the circles cannot break one another on meeting, and as the water is of the same quality all the way through, its parts transmit the tremor to one another without change of position. Thus the water, although remaining in its position, can easily transmit the tremor to the adjacent parts, these transmitting it to other adjacent parts, while its force gradually diminishes until the end."
Leonardo da Vinci, Manuscript A, Institute de France, Paris

We have all thrown pebbles into water and watched what happened but not all of us have observed what happens so eloquently as Leonardo did almost 500 years ago!
First Drawing
Before we go any further I want you to draw a football. Try to observe what you see in front of you or from your memory of the football shape. Please don't read on any further until you have tried to draw it.
Three examples
Three real life photographs of drawings of 'footballs' are shown below. Two are from street signs around the UK, and the last is from a shop window display (the shop was selling black-and-white photos of old football teams). It's obvious that they all tried to draw what they thought was a football but it's also obvious that they all failed in a fundamental way – they look flat, not round.



Please don't be put off or depressed if your football looked like one of these. Until we understood the structure of the football we made similar drawings.
The Problem
Even if we have seen a football many times we still have to rely on how we had observed the shape and the different types of coloured patches on the ball. Also of course one of the difficulties of drawing is that we are trying to put on 2 dimensional (2D) paper a representation of a 3D object, so perspective is also needed.
Saved by symmetry
There is no doubt that when you start to look more closely at the shape of the football it seems pretty complicated, we tend to get lost trying to follow all the patches going around the ball.
However we have a powerful concept to help us - symmetry. It is true that the shape is very complicated but it is very symmetrical - there are lots and lots of repeating patterns. If we can spot these patterns we can make use of it to really see what is going on. We need to understand and appreciate the symmetry because simply trying to remember the pattern is too difficult - hence the understandable difficulty people have had trying to draw it!
The Icosahedron
People have been fascinated by symmetrical shapes for thousands of years. Plato, the famous Greek philosopher, played around with simple 2D shapes such as triangles, squares and pentagons (5 sides) and used them to construct 3D objects.
By just taking triangles for example we can make some wonderfully symmetrical shapes. For example if we take 4 triangles we get a tetrahedron and 20 triangles gives us the icosahedron (see picture of the crystals). In all these wonderfully symmetrical objects all the faces are the same as each other, all the corners are identical to each other and all the edges are the same as every other edge. These are just 2 of the set of 5 famous Platonic solids that have these unusual symmetrical properties.

The structure of the Football - the truncated icosahedron (!)
The icosahedron has 12 corners and from the picture (below) we can see that there are 5 edges coming out from each and every one. If we imagine that we have a sharp saw and could cut-off each corner (say 1/3 of the way along each edge) it would leave a five sided hole behind - a pentagon.
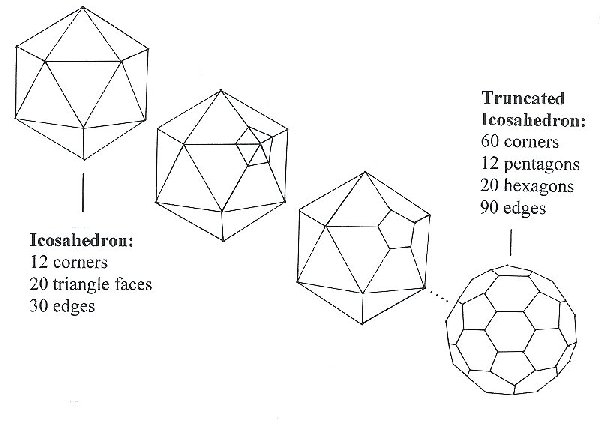
If we keep going round the shape, cutting off all the corners, we are doing what mathematicians call truncating the shape. As the icosahedron has 12 corners (each with 5 edges) truncating it produces 12 pentagons.
Also because about a 1/3 of the original edges are left behind (after cutting all the corners) we find that 6 sided shapes - hexagons – appear between these new pentagons. So by truncating the icosahedron we get a truncated icosahedron (!) which has pentagons and hexagons.
The truncated icosahedron is very symmetrical because the original icosahedron was so very symmetrical. Further to this it is exactly the same shape as a football!
Understanding the structure better
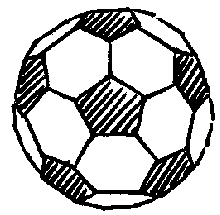
How can all this information help us to draw a football? Well if you look at a football (picture at the start of this article) you will see that although the hexagon (white) patches can be side by side we never see two pentagon patches touching each other (pentagons never share an edge).
In fact each pentagon (black patch) is separated from the next by hexagons. If you consider the symmetry and look carefully at a football you will see that every corner in the football resides in a pentagon (non are in a hexagon alone). As there are 12 pentagons and each pentagon has five corners then there must be 12 x 5 = 60 corners in the football.
Euler's Law
A famous mathematician Euler discovered a simple formula that accounts for the number of faces (F), corners (C) and the number of edges (E) in simple shapes:
He found that F + C - E = 2 for many shapes.
(where F, C and E are the numbers of face, corners and edges)
For example take a cube (die) it has 6 faces, 8 corners and 12 edges so we get 6 + 8 - 12 = 2, which works.
Now in a football we have 60 Corners and each corner has three edges (which themselves go between two corners). This means there are 3/2 edges for each corner giving a total for the whole ball of 60 x 3/2 = 90 edges.
Now we know we have:
C = 60, E = 90, F = number of Pentagons + hexagons = 12 + H
putting these in to C + F - E = 2 we can use it to predict the number of hexagons (H):
C + F - E = 2
60 + (12 + H) - 90 = 2
which on rearranging gives:
H = 2 + 90 - 12 - 60 =
20 hexagons on the football.
Pentagons
The pentagons are very important in the structure as we find that groups of hexagons can only be flat – just like a tiled floor (this is why the three pictures at the start of article look flat – they would be in real life). As each pentagon is added the shape curves up a little more. When 12 pentagons are included the ball completely closes up. When we draw the structure we need to take into consideration this curving.
Summary of the football - the truncated icosahedron
So from what we have learnt the football is a truncated Icosahedron having:
12 pentagons (five sided patches),
20 hexagons (six sided patches),
60 corners,
90 edges,
and although the hexagons can lie side by side no pentagons touch each other in this way (non share an edge).
Steps to drawing a football (see drawings below)
We can bring all that we have learnt together to help draw the football. Perhaps the simplest steps are shown below in the pictures:
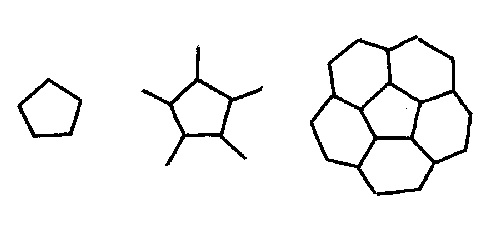
Above (from left to right):
1) First draw a regular pentagon.
2) Add lines away from each corner of the pentagon.
3) Add groups of three lines to form 5 hexagons surrounding the pentagon.

Above (from left to right):
4) Add more groups of three lines to make up 5 more pentagons on the outside (these pentagons are very distorted because they are curving away). So now we have 6 pentagons in total, half the total to be found going around the ball. As we can't see through the ball this is all the pentagons you need to draw.
5) Add curved lines (or groups of three lines if you prefer) to form the final (very distorted) hexagons on the outer edge of the ball. This completes the front side of the football as shown in the pictures.
6) Finally shade in the pentagons to make it look more like a football. Don't be scared to draw the lines in fast but make sure that each line is done confidently. This way the football will look like it is 'real'.
C60 - Buckminsterfullerene
In 1985 a new form of carbon was discovered having the same shape as a tiny football. An atom is to be found at each corner of the structure so it has 60 atoms. As C is the symbol for carbon it was called C60. The Molecule was named after the famous architect Richard Buckminster Fuller who designed large round dome buildings rather like half a football. The molecule was therefore called C60, or Buckminsterfullerene.
This new discovery is very exciting and is opening up new fields of science. Structures made of these carbon network of atoms are very light and extremely strong. In 1996 the Nobel Prize for Chemistry was awarded to the scientist discovers (Harry Kroto, Rick Smalley and Bob Curl) for this amazing work.
What we have learned here about the structure and symmetry of a football was crucial to the discovery of C60, because without it the scientists would not have actually understood the significance of what they had discovered!

Second Drawing
From what you have learnt about the structure of a football it should now be a lot easier to draw a football. Now make a drawing and compare it to the one you made at the start.
Summary
We have chosen to study a football in this article but what we have learnt could be applied to all sorts of symmetrical objects that we might want to draw. To improve our drawing skills we just need to remember to try and observe (really observe) what is in front of us – i.e. to see clearly the shapes, patterns and symmetries.
Acknowledgements
For inspiration and support I would like to thank Prof. Harry Kroto, the late Jan Meering (Angmering School), NESTA (The National Endowment for Science, Technology and the Arts) and the Campaign For Drawing (NESTA funded).

Questions
1) How many corners are there in the icosahedron and how many pentagons in a football?
2) Look back at the three photographs of pictures of footballs, now you know more about the structure of a football can you see what was wrong with the drawings?
Books and articles:
Leonardo - The First Scientist, Michael White,
Abacus, 2000. ISBN 0 349 11274 6
Perfect Symmetry, Jim Baggott,
Oxford, 1994. ISBN 0 19 855790 6
Shapes, Space and Symmetry, Alan Holden,
Dover, 1971. ISBN 0 486 26851 9
Platonic and Archimedean Solids, Dawud Abu-Asiya,
Wooden Books, 1998. ISBN 1 902418 03 4
web sites:
The Creative Science web site
Vega Trust Site (HWK at Manchester United Football Club)
Answers
1) Number of corners and pentagons is 12
2) The first and second picture only have hexagons while the last has squares and octagons but no pentagons or hexagons. None of these would be very good on the playing field as they are flat, not round!!
home | diary | whats on | CSC summary | latest news