Group Theory applied to C60, buckminsterfullerene
(adapted from Jonathan Hare's PhD thesis, Sussex University, 1993.)
Group theory can be used to determine the normal modes of vibration for C60.
From this we can predict the number of infrared and Raman active bands - 4 IR active bands (4T1u) and 10 Raman active bands (2Ag + 8Hg) ...
IR spectroscopy played a key role in the discovery of a method to produce C60 in large quantities (large enough to be able to do practical chemistry). The group theory analysis shown here therefore allows us to understand the molecule in a fundemental way. See a students view of the discovery for more details.
To determine the modes of vibration we use the standard method as described below. A three axis basis set is centred on each atom and the operations, found in the Ih point group tables, are applied so that the reducible representation can be determined. The whole analysis comes down to deciding which atoms are unmoved by the particular class of operation, and how the basis set is effected. The pictures show the various views of C60 which help to determine the character of the reducible representations. Studying the diagrams we find that apart from the E and s operations, all the atoms must be moved under the action of the operations, and so these operations must therefore have characters equal to zero i.e. X = 0.
The E operation will not move any of the atoms, or effect the basis set, and so the character will be X = (+1 +1 +1) 60 = 180. The reflection (s) will move all but four atoms, and each of these will have the basis set axis perpendicular to the plane of reflection, reversed. The character of this reducible representation will therefore be X = (-1 +1 +1) 4 = 4. The complete reducible representation for C60 is shown over the page.
The next step is to reduce these representations to the sum of irreducible representations using the reduction formula (see ref. at end of this page). As we have seen, many of the reducible representations for C60 have zero character which simplifies the calculation to those shown in the table. By way of example, some of the calculations have been shown in full. Consulting a full Ih point group table we see that the rotations and translations for the C60 molecule have T1g and T1u symmetries respectively. These modes need to be subtracted from the reduction formula results, so that only the vibrational modes are determined. When this is done we arrive at the complete irreducible representation for the normal modes of C60.
By noting which irreducible representation has the same symmetry as 1) the dipole matrix (i.e. those that belong to the same irreducible representation as x, y or z) and 2) the polarisability (i.e. xy, z2, x2-y2 etc.) we find that C60 will only have 4 IR active modes and 10 Raman active shifts (see below). As a consequence of the exclusion rule we also know that the IR frequencies will never coincide exactly with the Raman shifts.
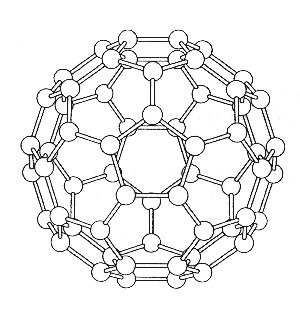
view of the C5, S10 and i symmetry elements
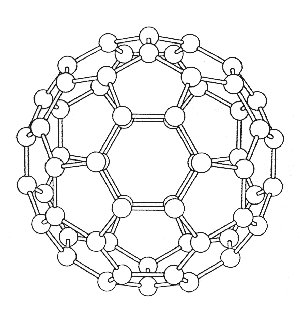
view of the C3 and S6 symmetry elements
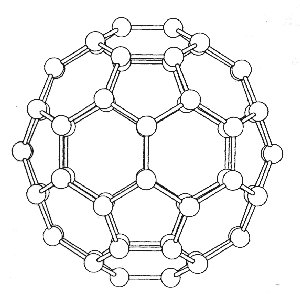
view of the C2 and σ symmetry elements
The reducible representations of C60 - Ih
|
E
|
12C5
|
12C2,5
|
20C3
|
15C2
|
i
|
12S10
|
12S3,10
|
20S6
|
15σ
|
|
180
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
4
|
The simplified point group table for C60 - Ih
(order h = 120)
|
Ih
|
E
|
15σ
|
|
=
|
180
|
4
|
|
Ag
|
1
|
1
|
|
T1g
|
3
|
-1
|
|
T2g
|
3
|
-1
|
|
Gg
|
4
|
0
|
|
Hg
|
5
|
1
|
|
Au
|
1
|
-1
|
|
T1u
|
3
|
1
|
|
T2u
|
3
|
1
|
|
Gu
|
4
|
0
|
|
Hu
|
5
|
-1
|
From the reduction formula, subracting the rotations and translations we get:
vibrations = 2Ag + 3T1g + 4T2g + 6Gg + 8Hg + 1Au + 4T1u + 5T2u + 6Gu + 7Hu
the normal modes with the same symmetry as a component of the dipole moment or as the component of the polarisability give:
4 IR active bands (4T1u) and 10 Raman active bands (2Ag + 8Hg)
NOTE: for more information and to learn about Group Theory please read and work through:
Molecular Symmetry and Group Theory, Alan Vincent, 1990, Pub. John Wiley, ISBN 0 471 01868 6.
Dr Jonathan Hare, E-mail: jphcreativescience@gmail.com
NOTE: Although none of the experiments shown in this site represent a great hazard, neither the Creative Science Centre,
Jonathan Hare nor The University of Sussex can take responsiblity for your own experiments based on these web pages.
THE CREATIVE SCIENCE CENTRE
home | diary | whats on | CSC summary | latest news


