Last time we looked at a little of the history of time keeping leading up to caesium atomic clocks and the LF radio signals, such as MSF on 60 kHz, that are used to broadcast time. Here we look in detail at how the time is encoded onto the MSF signal.
The MSF specifications
MSF consists of a 27kW CW transmitter producing an ERP of about 15 kW to a vertical omnidirectional antenna (located at Anthorn in the north of England) [1]. At a range of 1000km the signal strength should still be about 100uV/m so all of the UK and northern Europe are catered for. The carrier and its timing signals are derived by two caesium atomic clocks (with a Rubidium backup) accurate to 2 parts in 1012 which is a long term stability of about 1 sec in 50,000 years. The NPL web site has a summary of the MSF specifications [1].
Note: MSF is off-air a few times a year for general maintenance. A bulletin and e-mail service is available from the NPL giving advanced warnings of these down periods [2].
Time coded information
Every minute the MSF time code transmission sends the following data: year, month, day of month day of week, hour, minutes, BST / UTC and some astronomical information [1, 3]. Unlike other radio time signals MSF transmits two bits of data every second, called bit A and bit B. This is called the slow code. There used to be a fast code (all the slow code data was sent in the last second of each minute) but this was removed in 1998.
2 bit slow code: bit A and bit B
MSF sends data by dropping the 60 kHz carrier every second. At the start of each minute the carrier goes off for 0.5 seconds (500ms) and so is uniquely identified by this 500ms 'start bit'. The rest of the time the carrier only ever goes off for a maximum of 300ms. The second marker is transmitted with an accuracy of better than ±1 ms.
Bit A and bit B are transmitted in the following way [2]:
(bit A = 1 if set, bit A = 0 if not set)
* If the carrier goes off for 100ms then both bit A and bit B of that particular second are 'zero', 0, i.e. they are not set.
* If the carrier goes off for 200 ms then bit A = 1 and Bit B = 0.
* If the carrier goes off for 100ms then on for 100ms then off for a further 100ms then Bit A = 0 and Bit B = 1
* If the carrier goes off for 300ms then both Bit A =1 and Bit B = 1.
As two bits of data are transmitted every second then 2 x 60 = 120 bits of time information can be built up over the minuet. It is this data which the MSF clock decoder has to use to calculate the time information. The falling edge of bit A provides the seconds count. The seconds do not therefore need to be encoded onto the code. Most of the day-to-day time information is on the bit A data. However, on the 58th second bit B shows if the time is UTC (Greenwich, bit B = 0) or summer time (BST, bit B = 1).
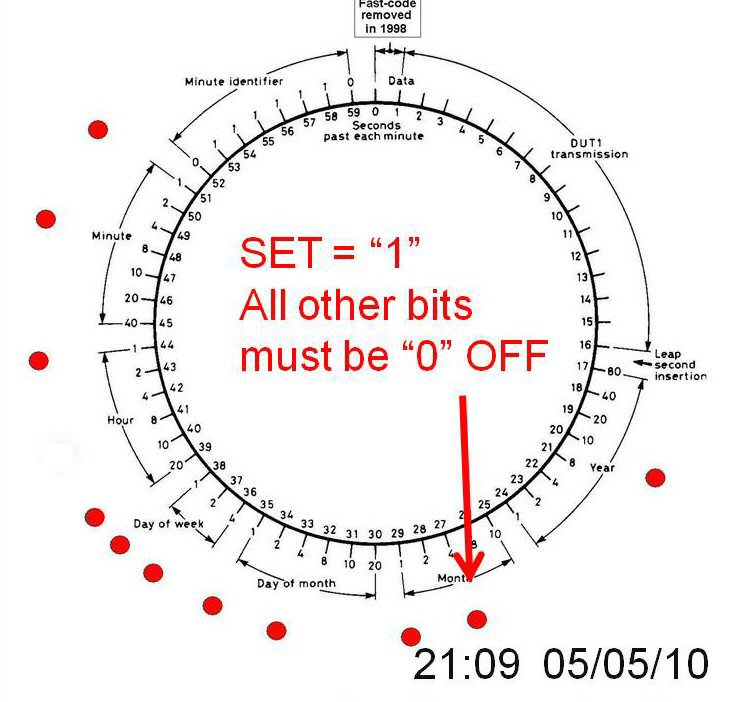
Fig. 1 Summary of the five possible CW signals sent every second on the 60 kHz MSF transmission by dropping the carrier. The time code is built up using a two bit slow code (bit A and bit B).
Summary of time information and bit A's
The first 16 or 17 seconds of the bit A data contains time data of interest mainly to the scientific and astronomical community. The rest of the seconds in the minute contain the following time information:
Seconds 17 to 24 of bit A contain the 'year' information. The bits are assigned different values using a binary coded decimal system. For example bit A of the 17th second has a value of '80', bit 18 = '40', 19 = '20', 20 = '10', 21 = '8', 22 = '4', 23 = '2' and the 24 second bit A = '1'.
25-19s of bit A: contain the month information (25 = '10', 26 = '8', 27 = '4', 28 = '2', 29 = '1')
30-35s of bit A: contain the 'day of month' information (30 = '20', 31 = '10', 32 = '8' 33 = '4', 34 = '2', 35 = '1')
36-38s of bit A: contain the 'day of week' information (36 = '4', 37 = '2', 38 = '1')
39-44 of bit A: hour (39 = '20', 40 = '10' ... 44 = '1')
45-51s of bit A: contain the 'minute' information (45 = '40', 46 = '20' .... 51 = '1')
52-59s of bit A: are always the same: 01111110. This pattern never occurs elsewhere in the code (whatever the time or date might be) so uniquely identifies the following second minuet market (start bit).
These bit values are used to calculate the time information by adding up the values of the bit A's that are set (i.e. that are 1). So for example if bit A is set "1" on the 20th second (a value of '10') but no other between the 18 and 24 seconds it means the year can be calculated as follows:
Year = value of bit 18 (if set) + value of bit 19 (if set) + …. Value of bit 24 (if set)
Year = (0 x 80) + (0 x 40) +(0 x 20) + (1 x 10) + (0 x 8) + (0 x 4) + (0 x 2) + (0 x 1) = 10
so the year is 2010
Note: In the case of a 'leap second' added (or taken away) from the year the extra seconds are incorporated (or removed) during the last minute of the year (59 or 61 seconds) and so the code is modified accordingly. As this only ever effects this one minute in the year I haven't built this into the PIC decoder and won't discuss this further. See the NPL data sheet for more details [1].
Typical time 'calculation'
Let's say it's 9-09 pm on Wednesday the 5th of May 2010, what would we expect for Bit A and Bit B data as it comes live from the MSF transmission? Looking at Fig. 2 [3] we can see the various values each bit A has around the minute. We can use this to assemble the time information from the data coming in from MSF or in this case work out what we should have for this particular date and time:
Year: 2010 = 10 so bit A is set 1 on 20th second, bit A = 0 for 17-19 and 21-24 seconds.
Month: May = 05 = 4 + 1 so bit A is set 1 on the 27 and 29th second,
Day of month: 5th = 5 = 4 + 1 so bit A = 1 for 32 and 35 second
Day of week: Wed = 3rd = 2 + 1 so bit A = 1 for the 37 and 38 seconds
Hour: 9pm = 21 hours = 20 +1 so bit A = 1 for the 39 and 44 seconds
Minutes: 09 = 9 = 8 + 1 so bit A = 1 for the 48 and 51 seconds
Fig. 2. Diagram showing the bit A data leading up to the start of 21:09 on the 5th May 2010. Bit A's that are set have a circular red marker next to them. All other bits should be zero (un-set) these are the main bits used to calculate the time information. Note: Bit B of the 58th second is also set 1 (not shown) as it provides the BST signal (UTC = 0, BST =1). [3]
Looking at Fig. 2 you can see the values of the various bit A's during the minute. In this example all the bit A's should be zero (0) apart from the following bit A's which will be set 1 at:
20, 27, 29, 33, 35, 37, 38, 39, 44, 48 and 51 seconds.
Note: the 58th bit B should also be set 1 as May is 'summer time' so the clock time is BST.
This is shown in the diagram. The red dots represent the set bits (bit A = 1) and where there is no red dot it means Bit A = 0, i.e. not set. It is precisely this simple type of calculation that the decoder has to do with the 60 seconds of bit A and bit B data logged from the MSF code. This calculation is done quickly by the processor during the last second of each minute so that the new time data can be loaded up on the screen (see the last article of this series for more details).
What you hear tuning in to 60 kHz
So if you were just happening to be listening to the CW signal from the MSF at this time you would have heard many sort drops in the carrier for the 0 set bits and longer drops for the seconds where bit A = 1. Some of the seconds may have been double drop outs corresponding to bit A = 0 and bit B =1 data being sent. The 58th second would have been a longer than average drop (300 ms) because it was summer time so bit B and bit A happen to be set 1.
Next Time
Next time we look at various antennas we can use to reliably pick up the LF 60 kHz MSF signal.
[3] the minute circle diagram shown in Fig 2 was taken (and modified) from Radio Data Reference Book , G. R. Jessop (G6JP), 5th edition, 1985, RSGB. ISBN 0 900612 67 3
THE CREATIVE SCIENCE CENTRE
Dr Jonathan Hare, The University of Sussex
Brighton, East Sussex. BN1 9QJ.
