There are at least two things that define a scientist. First, we do experiments based on our ideas / theories to explore and understand the things we see around us. An experiment is a rather contrived situation where we try and arrange things to be as constant as possible apart from one aspect that we carefully change. Then we usually look for a change in a value (a number) of one of measurable quantities. Second, we try to realistically understand these numbers generated by the experiment. The experiment is like a question and the result is an answer, perhaps hidden, in the generated numbers. Scientists like this sort of a puzzle.

This all sounds a bit technical but in reality these "numbers" are usually based on things we can measure that help us see things clearly, such as 1, 2, 3 of course, or perhaps ON, ON, OFF, or greater or less, perhaps a light or dark band in an optical experiment. In other words, numbers are something that help clarify whatever it may be that we are trying to observe. Without numbers the picture can be fuzzy, indistinct and capable of being misinterpreted. With numbers the image starts to sharpen. Maths allows us to express observations with great precision

Clear observation is at the heart of all this: to try to see what is really in front of us, rather than what we might think or hope is there. Using maths we can be very specific about what we see, and then start to spot patterns that would be difficult to perceive otherwise. You could say that maths is the science of patterns [1].

Maths - to an experimenter
At school I had reading and writing problems and so I tended to learn things by studying diagrams, pictures and playing with machines. For example I learnt electronics by "reading" 100s of diagrams and making 100s of circuits. Sometimes I would make what looked like a perfectly reasonable circuit but it just wouldn't work — this puzzled and bothered me. When I got to university we learnt about the theory — the maths — that was involved. Although I could often work things out by experimenting I found that making an effort to understand the maths often made it profoundly clearer. When I re-worked the rogue circuits with what I had learnt from the maths they worked!

It was a very direct way of seeing why maths is so powerful. It was really exciting - in fact it was wonderful. Experimenting with electronics was a bit like finding a treasure island full of exciting things. Later, learning the maths theory was suddenly like being given the map to this treasure island!

It was only when I learnt the maths theory that I really started to get a broader understanding of what I was doing when I was soldering all those components together.

Maths in research – C60, Buckminsterfullerene
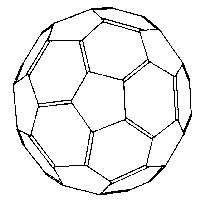
In 1985 a fabulous 60 atom carbon molecule called C60, Buckminsterfullerene, or Buckyball, was discovered in tiny amounts. C60 has the same shape as a soccer ball, all-be-it 100 million times smaller. It was a serendipitous discovery which is now revolutionising nano-technology. In 1996 its discoverers were awarded the Nobel Prize for chemistry. My PhD work was on making test tube quantities of C60.

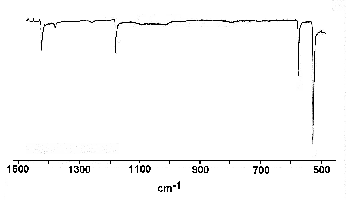
We used a technique called infrared (IR) spectroscopy to search for C60. Atoms in molecules vibrate due to their thermal energy; this is what heat is. Molecules can absorb Infrared (IR) energy because of some of these vibrations, these movements. In general each atom can vibrate in 3 dimensions so something with 60 atoms will have a maximum of 3 x 60 = 180 vibrations. Only certain groups of these atomic motions will physically have the correct motions to interact with the IR energy and so only these will contribute to the molecule absorbing in this part of the spectrum.

Group theory is a mathematical technique that allows all the different possible combinations of atom movements to be accounted for. When you apply group theory to a 60 atom carbon molecule with no basic shape or symmetry it comes out with about 176 absorptions. This would produce a very complex IR spectrum and so would be difficult to search for. If we apply the technique to a more symmetrical 'flat sheet' of 60 atoms it predicts 25 IR bands. When we apply the maths to the very symmetrical football shaped C60 it predicts just 4 IR absorptions [3]. This crucial piece of information meant we could start a practical search — and using this we found it. Only maths can predict the 4 line absorption of C60!

Without that piece of reliable information it would have been like looking for a needle in a hay stack. Without this piece of maths the investigations would have probably got more complicated rather than more elegant

Maths in education - the shake-a-gen
In one of my Gifted and Talented workshops [2] the children make a simple electrical generator. It consists of an empty film can, a strong magnet, some wire and an LED light bulb [4, 5]. The children wind the wire around the can and connect the two ends to the LED light. The magnet is put inside the can when they shake it the magnet moves in an out of the coil converting the mechanical energy into electrical energy so lighting the LED light

The question is how many turns of wire do the children need to wind onto the can? The answer can be found by hours and hours of trial and error or in just a few seconds using maths. The voltage (V) produced is dependant on the Area of the coil (A), the strength and rate you can shake the magnet (B) and the number of turns of wire (N). In maths terms it's pretty simple: voltage = V = A x B x N or in terms of the number of turns N = V / (A x B).

Using some basic data the children can use the equation to work out the number of turns they need to wind around the can which comes out at 1000 turns. Before I give them the magnets I ask them "what if you miscounted by say 10 turns so that you actually have 990 or 1010 turns on the coil. What difference will this make?"

The answers I get back are very revealing. Those who found the maths quite easy tend to realise that missing 10 turns is only a small amount of the total (only 1%) and usually feel confident that it probably won't make much difference to the LED brightness. Those who didn't have the maths skills however tend to be a bit lost - they don't quite know what to think

Without the maths the children would probably give up trying to get the LED to light as 100 to 200 turns simply do not generate enough electricity to get the LED to glow. The maths lets us leapfrog over guesses taking us directly into a region where success is likely.

Why maths is so important
In the process of trying to make science appeal to a wider audience it can often be presented with much of maths removed. There may be some justification for this in the early stages of education. The problem is that this may actually be the best time to learn these maths skills to set them up for later. School children may well be getting a broad outline of science but by restricting the maths it may make it harder for them to learn how to estimate properly and to know what information is reliable.

Maths is not necessarily appropriate to every aspect of life. In a complex world however, it can simplify things and help you decide if a piece of information is reliable or not. Reliable information is something very, very precious to humanity.

While putting this article together I wrote to colleagues in various different scientific fields for their thoughts and comments about maths:

Prof. Slobodan Danko Bosanac, Physist
Mathematics is an excellent slave but a very bad master … someone once said that statistics is not for enlightenment but should be thought as a support … like a lamppost is to a drunken man.

Prof. Norman Billingham, Chemist
The best thing I can say is that in 40+ years of working as a researcher in physical chemistry I've never met anyone who didn't wish that he knew more maths.

Neill Jones, Computer Programmer
Numeracy and an understanding of statistics has been of benefit when it comes to understanding when politicians are bending the truth. An understanding of probabilities has been useful in assessing risks … and knowing that betting on the lottery is a pound badly spent.

Chris P., school boy experimenter (dyslexic)
I find maths very impotent [important] in my exsperaments and i do like maths. I find math exspesarly useful in my mecanical tv exsperaments as you need to get the right timeing betwine the input vidio signal and the speed of the disc. math is also important when i am disianing [designing] my new exsperaments and when im doing tecnical drawing it is inportant as if it is one mill off the hole exsperament can be rewend [ruined].

Dr Bernd Eggen, Climate Scientists, Met Office UK
Mathematics and statistics underpin all areas of climate science and help make the results robust.  The mathematical formulae that describe the interactions of the atmosphere with other components of the Earth's climate system are the basis for climate models - typically these equations are very complex and require supercomputers to solve them.  Statistics plays a crucially important role in attribution & analysis of climate change, to separate the signal from [other factors and] noise.

Dr Simon Outram, Epidemiology Scientist
Mathematics are well beyond me, but statistics provide an excellent starting point for the scientific investigation of the distribution of diseases across the world's populations.  However, they are also the source of a considerable temptation - confusing and equating statistical association with biomedical causation

Sir Harry Kroto, Chemist, Nobel Prize 1996
If one wants to understand English Culture, say the deeper creative aspects from Shakespeare to Pinter it stands to reason that one really needs to learn English. Analogously, if one really wants to understand the deeper cultural meanings of the Sciences the beautiful relationships that underpin the workings of Nature and the Physical World - Physics in particular whose language is Mathematics - one really does have to learn Mathematics. To those who say that one should be able to explain Science without Mathematics I respond: "Do you think we use mathematics to make life harder for ourselves? No we use it because it is the only way to understand it - It's not my fault, there really is no other way!

Russel Taylor, Engineering teacher in a USA College
"America's current (recession) problems are a direct result of not knowing enough maths!"

References
[1] Mathematics, Keith Devlin, Sci. Am. Lib, 1997. ISBN 0 716760223
[2] The CSC web site: www.creative-science.org.uk
[3] J P Hare Phd Thesis, Sussex University 1993, also see CSC web site URL above
[4] The shake-a-gen J. P. Hare, IOP press, Journal of Physics Education, September 2002, p.436-439.
[5] for short educational science movies please see the : Vega Trust web site